الأنظمة البلورية

من أجل تحديد الإرتباط بين الأوجه البلورية للشكل البلوري وتعريف وضعها في الفراغ يجب القيام بذلك من خلال مجموعة من الخطوط التصويرية (ثلاثة أو أربعة) تتقاطع مع بعضها البعض في مركز تماثل البلورة، وتسمى هذه الخطوط بالمحاور البلورية كما يتضح في الشكل التالي ويشار إليها بالرموز أ، ب ، جـ حيث تحصر بينها الزوايا التالية:

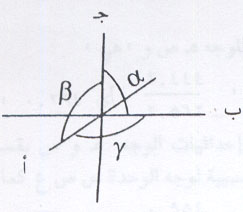
α (ألفا): وتقع بين المحورين ب، جـ.
(بيتا): وتقع بين أ ، جـ.
(جاما): وتقع بين أ ، ب.

وتنقسم البلورات حسب اختلاف عناصر التبلور (محاور بلورية والزوايا بينهم) إلى سبعة أنظمة بلورية هي:

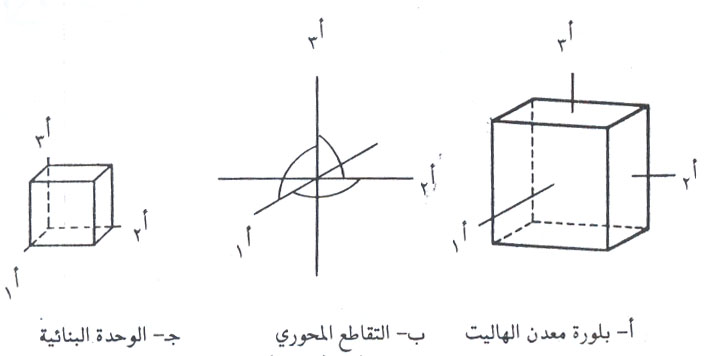
1- النظام المكعب

يضم هذا النظام جميع البلورات التي تكون فيها المحاور البلورية متساوية ومتعامدة أي أن أ = ب = جـ والزوايا المحورية α = = =90 °.

يتم تقسيم الأنظمة البلورية الى أصناف بلورية حيث تنقسم الأنظمة البلورية السبعة الى 32 صنف بلوري إعتماداً على إختلاف درجة التماثل بين كل صنف وآخر ضمن نفس النظام البلوري، نستطرق معكم إلى إحداها وهو الصنف الكامل التماثل كما يلي.

الصنف الكامل التماثل:

الصنف السداسي الثماني الأوجه هو الصنف الكامل التماثل في نظام المكعب.

قانون التماثل لهذا الصنف هو : 4 ³ /م 3 ⁴ 2 ⁶ /م ن.

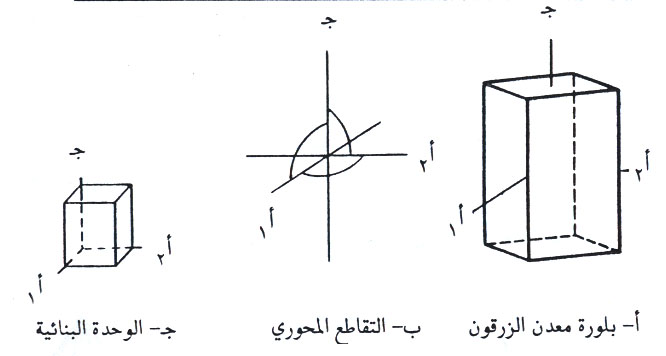
2- النظام الرباعي

ويكون فيه أ = ب = جـ والزوايا المحورية α = = =90 °.

عناصر التماثل:

تتميز جميع بلورات النظام الرباعي بوجود المحور الرباعي التماثل الى جانب عناصر التماثل الأخرى التي يتم بوجودها تقسيم النظام الى سبعة أصناف بلورية.

الصنف الكامل التماثل:

الهرم الرباعي المزدوج هو الصنف الكامل التماثل في النظام الرباعي. قانون التماثل الكامل له هو: 4/م 2 ⁴ /م ن.

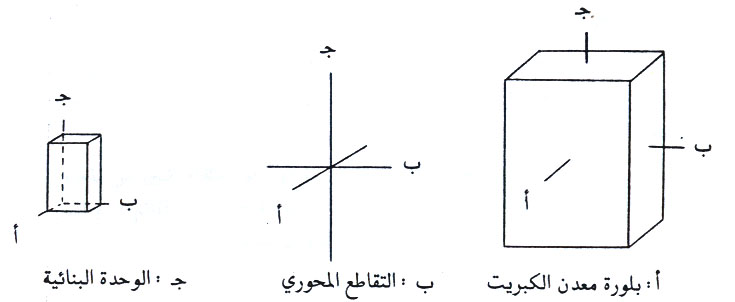
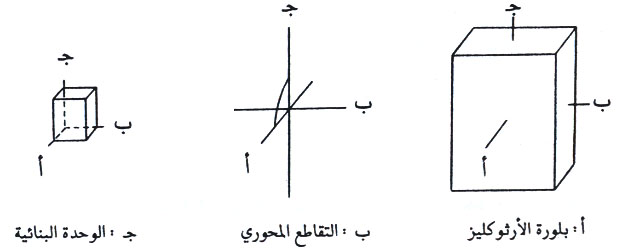
3- النظام المعيني القائم

وتكون علاقة المحاور البلورية والزوايا كالتالي: أ = ب = جـ والزوايا المحورية α = = =90 °.

الصنف الكامل التماثل:

صنف الهرم المنعكس المعيني القائم هو الصنف الكامل التماثل في النظام المعيني القائم. قانون التماثل لهذا الصنف هو: 2 ³ /م ن.

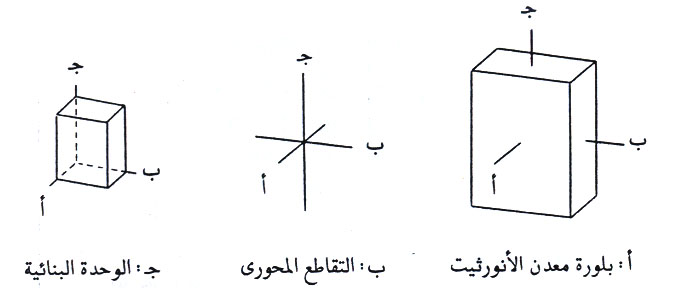
4- النظام أحادي الميل

يتم تغيير قيمة زاوية واحدة هي الزاوية لتصبح أكثر من 90 ° مع بقاء الزاويتين الأخريتين = 90 ° كما أن الأطوال البلورية غير متساوية أي أن أ = ب = جـ والزوايا المحورية α = = 90 °، =90 °

الصنف الكامل التماثل:
صنف منشور الميل الواحد هو الصنف الكامل التماثل في نظام أحادي الميل ويتميز بوجود محور واحد ثنائي يتعامد على مستوى تماثل. قانون التماثل لهذا الصنف: 2/م ن.

5- نظام ثلاثي الميل

يتم تغير الزوايا المحورية الثلاثة α ، ، لتصبح زوايا منفرجة، بالاضافة الى أن المحاور البلورية الثلاثة غير متساوية الطول.
أ = ب = جـ والزوايا المحورية α = = =90 °.
الصنف الكامل التماثل:
نظام مسطوح الميول الثلاثة هو النظام الكامل التماثل في هذا الصنف. قانون التماثل لهذا الصنف هو: ن.

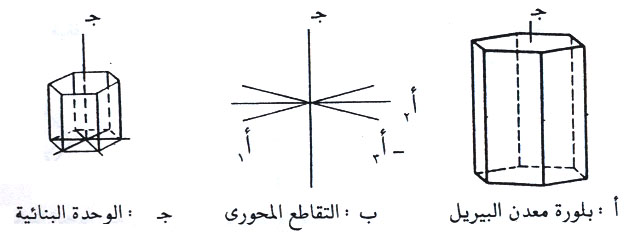
6- النظام السداسي

وجود المحور السداسي التماثل في هذا النظام يتطلب وجود ثلاثة محاور بلورية أفقية متساوية هي أ­1 ، أ2 ، أ3 تنحصر بينها زوايا مقدارها 120°، الى جانب المحور الرأسي جـ المتعامد على هذه المحاور الأفقية، ويكون إما أقصر أو أطول منها وينطبق على المحور السداسي التماثل.

وبناءً على ذلك تصبح عناصر التبلور هي أ1 = أ2 = أ3 = جـ والزوايا المحصورة بين المحاور الأفقية وبعضها تساوي 120 ° وبين المحاور الأفقية والمحور الرأسي جـ تساوي 90 °.

الصنف الكامل التماثل:
صنف الهرم المنعكس السداسي المزدوج هو الصنف الكامل التماثل في نظام السداسي. قانون التماثل لهذا الصنف هــو: 6/م 2 ⁶ /م ن.

.

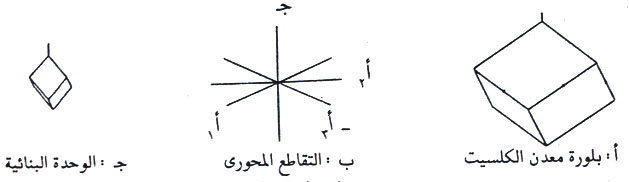
7- النظام الثلاثي

هناك تشابه بين نظامي الثلاثي والسداسي، فهما يشتركان في عدد المحاور البلورية، وعلاقة هذه المحاور بعضها ببعض. ويتميز النظام الثلاثي بوجود محور ثلاثي التماثل وكذلك عدم وجود مستوي تماثل أفقي بها. لذا فإن عناصر التبلور في هذا النظام هي: أ1 = أ2 = أ3 = جـ والزوايا المحصورة بين المحاور البلورية الأفقية 120°.

الصنف الكامل التماثل:
صنف مثلثي الأوجه الثلاثي المزدوج هو الصنف الكامل التماثل وقانون التماثل هـــو: 3 2 ³ /م.